Example 3

Example 3: Computing Implied Foreign Rates from a Currency Forward Price

The objective of the following exercise is to illustrate how the covered interest rate parity theorem applies to the real world markets. In this application we will apply the FTS Futures Calculator to infer the Euribor (or Eibor as it is also referred to) which is the euro benchmark in continental Europe . This is the offshore deposit rate that is the benchmark for estimating arbitrage free prices across markets from. As a result, under the assumption that derivative prices are arbitrage free it is possible to infer the deposit rate from the actual derivative prices.

Consider the following data:

On Dec 20, 2002 the following relevant data is obtained from the mid point of the bid/ask spread and the forward points bid/ask spread:

Spot Rate (USD/EUR (Currency in USD)): 1.0269

30 Day Forward 1.0254

60 Day Forward 1.024

90 Day Forward 1.0228

Spot Rate (EUR/USD (USD in Currency)): 0.9738

30 Day Forward 0.9752

60 Day Forward 0.9766

90 Day Forward 0.9777

Money Rates: Late London LIBOR

1 Month 1.4%

3 Month 1.4%

6 Month 1.46%

12 Month 1.51%

Question: What are the implied Euribor rates (in continuously compounded form) given the above currency forward rates?

To answer this question we apply the covered interest rate parity relationship to the spot and forward markets using LIBOR as the USD offshore deposit rate and solve for the implied Euribor offshore deposit rates.

Step 1: Launch the FTS Futures Calculator from the virtual classroom and select Calculator from the menu items as illustrated below.

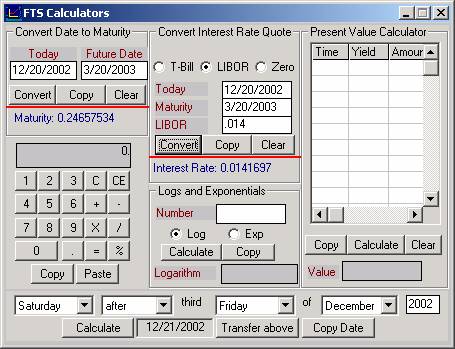
We first convert the USD LIBOR to continuously compounded form. Select LIBOR and enter the 3-month spot LIBOR rate as a decimal and then click on Convert. The implied continuous compounded rate is provided as follows (0.0141697):

Step 2: Launch the FTS Futures Module from the Virtual Classroom and enter the following information:

Remark: You can enter dates directly or you can enter the date as a decimal time to maturity. The decimal time to maturity can also be calculated using the FTS Calculator in step 1 if you want to. This is not necessary, however, because the date can be entered directly as illustrated below:

Important Note: When applying the Cost of carry model to solve for the currency forward price or an implied input, there are two interest rates required. The domestic rate and the foreign rate. However, domestic and foreign rates are relative terms and so the “domestic rate” is the cost of financial carry in the currency the price is measured in. This is because the synthetic forward requires borrowing in the currency the price is measured in at the domestic rate, converting at the spot rate and depositing at the other rate of interest. As a result, the “foreign rate” is equivalent to a dividend from this deposit. In the FTS Futures Calculator the dividend yield is the foreign rate of interest for a currency forward.

Required Inputs to Calculator to Solve for the Implied 90-day Euribor rate of interest (continuously compounded).

Spot Rate (USD/EUR) 1.0269

USD LIBOR rate (90-days continuously compounded)) 0.014697

Quote date 20/12/2002 , Maturity date 20/3/2003

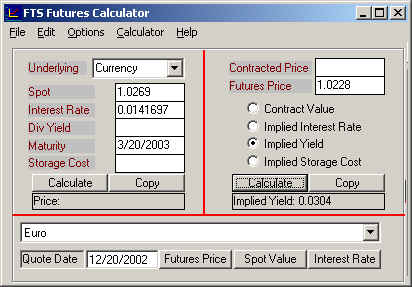
Screen 1: Entering dates (Quote Date and Maturity Date (alternatively you could enter the decimal time to maturity beside maturity if you want to) directly, and solving for the implied foreign rate (Dividend Yield) directly. In the right hand side of the screen click beside Implied Yield:

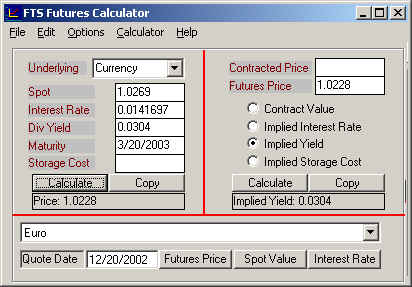
Screen 2: Verifying that the implied foreign rate supports the observed market price of 1.0228. To do this in the screen below we will enter 0.0304 directly beside the Div Yield and then calculate the price by clicking on Calculate. You can observe the answer is provided on the left side of the screen.

Step 3: Interpretation

Observe that covered interest rate parity relationship implies that the forward points must favor the USD because interest rates are lower in the US than in Europe (as of the 20 December 2002 ). In the supporting arbitrage argument the following two alternatives must be identical:

i. Deposit $1 at USD LIBOR for 90–days, or

ii. Convert $1 at the spot exchange rate (= EUR/USD euros), deposit at Euribor (1+Euribor*90/360) for 90-days and at the same time enter into a 90-day forward contract to convert (EUR/USD*(1+Euribor*90/360) Euros to USD in 90-days.

Both i. and ii. can be executed at the same time and both result in USD at the end of 90-days. As a result, both should result in exactly the same number of USD to avoid creating an arbitrage opportunity. But this implies that the spot and forward rates must be consistent with the deposit rates for each country. If the USD deposit rate is lower than the Euro deposit rate then the forward rate must adjust so that the USD is priced to appreciate against the Euro. You can see this by contrasting the spot exchange rate (1 euro buys 1.0269 USD on December 20, but in 3-months time 1 Euro is exchanged at 1.0228 USD in the forward contract. That is, 1 euro buys less USD in 3-months time at this forward rate. The amount less exactly compensates for the difference between the two 3-month deposit rates.

Step 4: Additional Question: How does the way exchange rate are measured matter?

To answer this question we will repeat the above exercise by working with EUR/USD and assuming that the 90-day continuously compounded deposit rate for the Euro is 0.0304.

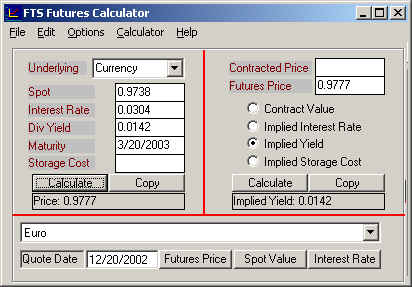
In this exercise the domestic rate is now the Euro rate (0.0304) and the foreign rate (i.e., dividend yield) is the USD rate (0.0142). The right side of the screen computes the implied Yield (which in this case is the USD Libor rate continuously compounded) and in the Left side of the screen we enter this rate directly to verify the forward price.

Thus it does not matter which unit of measure you work with (i.e., USD/EUR or EUR/USD) so long as you are consistent in the application of the inputs.