previous topic

Example 2: Estimating the Dividend Yield for the Underlying Index

An immediate problem that arises, especially for a broad based index, is how do we estimate q? One approach is to forecast q from the constituents of the underlying index. This is difficult and relies upon forecasting the dividends for each stock in the index. Alternatively, you can use market prices to infer q at a point in time using Futures Calculator.

Exercise: Inferring the Markets Estimate of the Dividend Yield for an Index

What is the implied continuously compounded dividend yield for the S&P 500 on November 14, 1996 relative to LIBOR?

There are many alternatives to LIBOR for selecting the appropriate interest rate from the fixed income markets. For example, three contenders are the t-bill rate with the same maturity, the repo rate for Treasury paper and the Eurodollar market (for example see Bond Tutor for a discussion of these markets). The appropriate choice is determined by the lowest cost arbitrage transactions to support the cost of carry forward pricing model.

In this current example we illustrate the use of the London Interbank Offered Rate (LIBOR). Quoted LIBOR is stated in add-on interest form and thus must be first converted into it’s continuously compounded equivalent. You can find LIBOR in the financial press. For example, the Wall Street Journal quote LIBOR daily in a column currently headed Money Rates. You can also find LIBOR rates freely on the Net by searching for the London Interbank Offering Rate.

On November 14, 1996 the quoted 1 month LIBOR was 5 3/8% and the 3-months quote was 5 ½%.

November 14, 1996 Market Data:

Futures price (F) = 739.25, spot index (S) = 735.88, time to maturity (T) = Dec 21, 1996 and current time is November 14, 1996.

By using F, S, r and T our goal is to infer the markets estimate for the continuous constant dividend yield.

Step 1: Launch the FTS Futures Calculator from the Virtual Classroom page.

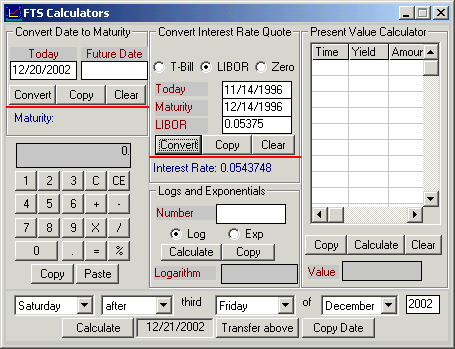
Step 2: Convert LIBOR to a continuously compounded pure discount rate. For a $100 invested today at the 30 day LIBOR rate of interest (5 3/8% for 1-month) equals $100 * 1.05375*30/360 = $100.4479 at maturity. Note this takes into account the daycount convention for LIBOR (i.e. actual over a 360 day year). To convert this into a continuously compounded rate of interest solves the following problem.

The continuously compounded equivalent of 5 3/8 relative to a 365 day year such that the present value of $100.4479 = $100? The answer is 0.05437 because $100.4479 * (exp(-0.05437*30/365)) = $100.

You can use the FTS Calculator (see menu item Calculator in the Futures Calculator) to convert the LIBOR quote directly into the implied continuously compounded rate for you.

To do this click on menu item Calculators above and enter the following information:

Note: Interest rates are entered in decimal format.

The LIBOR rate is 0.05375 in add-on interest quotation form. The implied continuous compounded rate is 0.05347 as indicated below.

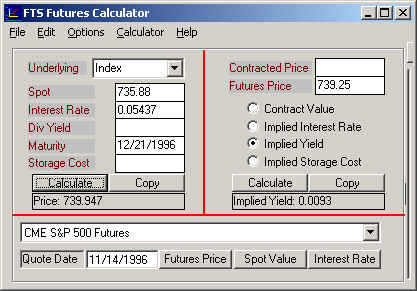
Step 3: Calculate the Time to Maturity for the futures contract by directly entering the dates, November 14, 1996 and maturity time December 21, 1996.

Step 4: Update your futures calculator with both the Spot Index value (Beside Spot type 735.88) and the Market Price (739.25). Turn on Implied Dividend Yield, by clicking beside it, and then click on the Calculate button. This computes the implied dividend yield (0.0093) from the futures price as follows:

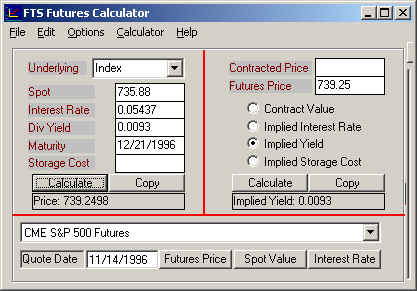
Step 5: To understand what you have accomplished consider the problem in reverse. What is the predicted futures price if the spot price is 735.88, the continuously compounded interest rate is 0.05437 and the dividend yield is 0.0093? Answer: 739.25. Fill the dividend yield into the calculator and check the result.

It is noted that the above estimate does not reflect the true dividend distribution over time but rather the constant continuously compounded rate relative to LIBOR for the underlying index.

Marking-to-Market

Index futures contract, like other futures contracts, are marked to market on a daily basis. Buying or selling a futures contracts requires an initial performance bond deposit to cover the risk of subsequent loss. In addition, a maintenance performance bond deposit is required as extra collateral. These bonds are deposited in special accounts controlled by the clearing house. Marking a position to market at the end of each day means that money is added to one performance bond account and deducted from the other. That is, a daily transfer takes place between the buyer and sellers accounts. You can access realized profits in your account so long as required levels are maintained. However, it is noted that if a balance drops below the required floor a performance bond call is triggered to bring this account back to the initial performance bond level (not the floor).

The extent to which marking-to-market is a factor for pricing a futures contract depends upon the extent to which the futures price systematically changes with shifts in the yield curve. This is because the opportunity cost associated with realized gains and losses can be measured by the interest foregone or received. For the case of deterministic interest rates marking-to-market has no effect, but deterministic interest rates is not a reasonable assumption to apply especially in an economy where interest rate policies are a tool used by the Federal Reserve Bank, for implementing economic policy. However for the same reasons as discussed in the last chapter, we will assume that the effects of marking-to-market are small for a Stock Index future. That is, we will assume that their value is given by the cost of carry forward pricing model.

That is, the value of the index future is the future value of one unit of the spot at the time of settlement. For example, one unit of the Standard and Poor’s 500 index future (traded on the Chicago Mercantile Exchange) is defined as $500 times the S&P 500 index. It is traded in points with a minimum tick size of 5 points (= 0.05 * $500 = $25 for 1-contract). For the case of an index future the valuation problem is complicated by the fact that the future value takes into account all dividends paid (i.e. ex-dividend dates) over the life of the future. This is because a cash market hedge receives dividends which serve to reduce the opportunity cost of funds tied up in the cash market. Thus, the future value is computed using the risk free rate of interest net of the rate of dividends received. Finally, an index future is defined on a financial and thus we can assume that the storage costs are zero. Together these comments imply that the value of an index future is:

where F is the futures price, S is the spot index value, r is the opportunity cost of the “carry” in the cash market (continuously compounded) and q is the continuously compounded equivalent of the dividend yield from the index. This last input is what you learned to compute from market prices in the above example.